Priemgetallen spelen online letterlijk een sleutelrol. Maar voor hoelang nog?
Onze veiligheid op het internet wordt gewaarborgd door versleuteling. De methode die hiervoor gebruikt wordt berust op de aanname dat priemgetallen nog geheimen hebben. Wat zijn de gevolgen voor onze veiligheid wanneer de bedachte versleutelingsmethoden zijn gekraakt?
Ontbinden in priemfactoren
Wachtwoorden worden in een database opgeslagen via versleuteling. Via methoden zoals RSA, een algoritme bedacht door Ron Rivest, Adi Shamir en Len Adleman. Het gebruikt de formule: n = p x q, waarbij de factoren (p en q) priemgetallen zijn. N, de product van p en q, wordt een RSA-getal genoemd. Omdat p en q, priemgetallen en factoren zijn, noemen we deze priemfactoren.
Een priemgetal is een natuurlijk getal groter dan 1, met precies twee delers. Controleren of een getal een priemgetal is kan als volgt: voor de delers gebruik je de waarden 1 t/m het getal zelf. Elke deler wordt gebruikt om een restwaarde te vinden. Zijn er precies twee delers, zijnde 1 en het getal zelf, dan is het getal een priemgetal. Deze methode wordt ‘Trial Division‘ genoemd.
Door de ‘zeef van Eratosthenes’ wordt “Trial Division” minder arbeidsintensief. De zeef begint bij 2. Elk getal is deelbaar door 1 en maakt die controle overbodig.
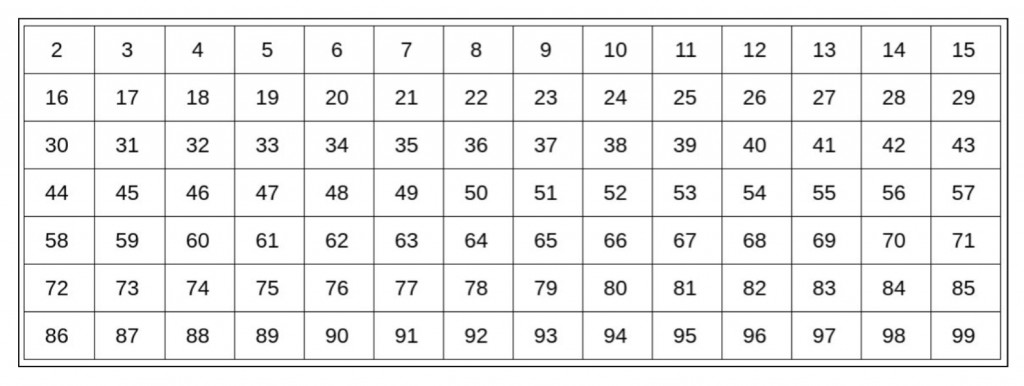
De zeef werkt als volgt: neem het eerste getal en streep alle veelvouden weg. De getallen 4 en 6 zijn veelvouden van 2. Een getal deelbaar door 6, is ook deelbaar door 2. De afbeelding hierboven is de startsituatie en de afbeelding hieronder toont het resultaat na toepassing van de zeef.

Ongeveer 26% van de delers blijft over door alleen de getallen 2, 3, 5 en 7 te gebruiken. Deze delers zijn allemaal priemgetallen. Bij de controle of een getal een priemgetal is, worden priemgetallen gebruikt.
Bovenstaande controle werkt snel, maar niet snel genoeg voor het controleren van grote getallen. Neem het getal 6.821.097.528.484.087, een getal met 16 cijfers. Met als laagste priemgetal 82.589.933, zijn 4.811.740 delers nodig om te bewijzen dat 6.821.097.528.484.087 geen priemgetal is. Het project Great Internet Mersenne Prime Search (GIMPS) heeft als doel steeds het grootst bewezen priemgetal te vinden. Er zijn een oneindig aantal getallen, hierdoor ook een oneindig aantal priemgetallen. Sinds 1996 heeft GIMPS steeds het grootst bewezen priemgetal gevonden. De formule die GIMPS gebruikt is 2^p -1, waarbij p een priemgetal is (let op: het toepassen van deze formule levert niet altijd een priemgetal op). Op het moment van schrijven is het grootst bewezen priemgetal 2^82589933-1, een getal met 24.862.048 cijfers.
Rivest, Shamir en Adleman
RSA maakt gebruik van de formule: n = p x q. Hierdoor belichaamt een RSA-getal (n) een eigenaardige eigenschap van priemgetallen. Het is makkelijker te bewijzen of een getal een priemgetal is, dan het vinden van beide priemfactoren (p en q). Deze eigenschap wordt gebruikt voor versleuteling. Om te bewijzen dat 6.821.097.528.484.087 (n) geen priemgetal is, zijn maximaal 4.811.740 delers nodig. Het bewijs dat 82.589.933 (p) een priemgetal is, kost 1127 delers. Om te bewijzen dat een oneven getal tussen 50.000.000 en 60.000.000 een priemgetal is, zijn ongeveer 945 delers nodig per getal. Het controleren van deze 5.000.000 oneven getallen, kost maximaal 4.725.000.000 delers.
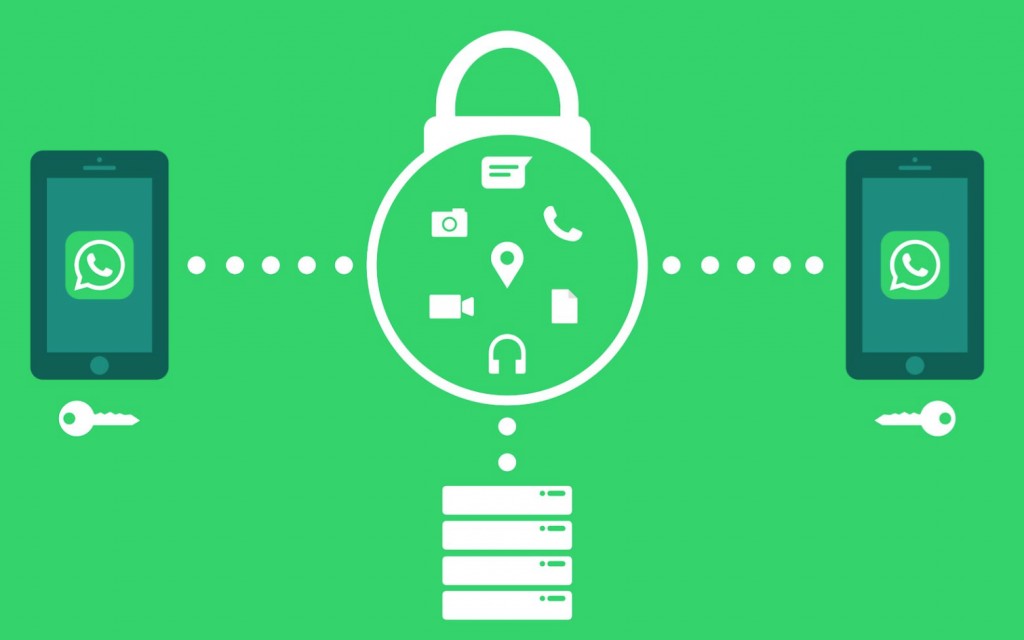
De afbeelding hierboven toont het versturen van een versleuteld bericht. We vertalen het naar een opdracht voor het overboeken van geld, waar jij de verzender bent en de bank de ontvanger. De opdracht wordt versleuteld met de publieke sleutel, een RSA-getal (n) gekozen door de bank. Websites of software downloaden de publieke sleutel en versleutelen je opdracht. Gearriveerd bij de bank, wordt deze omgezet naar de originele opdracht. Met een privé-sleutel die alleen de bank kent. Banken gebruiken een 2048-bits code, een getal van 617 cijfers. Dit wordt gebruikt als het RSA-getal (n). De priemfactoren (p en q) zijn hierdoor ongeveer 308 cijfers. De beschreven uitleg is een versimpelde weergave van de werking van RSA. Voor het versleutelen en ontsleutelen worden nog andere waarden gebruikt, die berekend worden via de priemfactoren (p en q).
Realisatie
De controle van 5.000.000 oneven getallen tussen 50.000.000 en 60.000.000, kost maximaal 4.725.000.000 delers. Getallen die wij begrijpen. De priemfactoren (p en q) van een RSA-getal (n), van een 2048-bit code zijn ongeveer 308 cijfers lang. Een getal dat moeilijk te bevatten is. Zelfs met de rekenkracht van de snelste computers, is het onbegonnen zaak om deze getallen te raden. Daarom is een RSA-getal (n) geen geheim. Een onderdeel van onze veiligheid en privacy is ‘publiekelijk’ bekend. Dit geeft aan hoeveel vertrouwen er is in de gebruikte versleutelingsmethode.
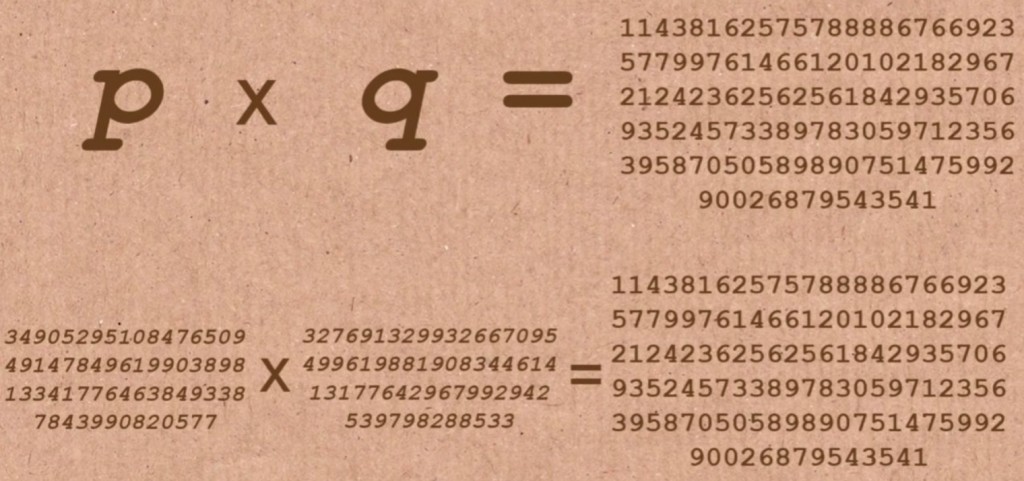
Gekraakte versleutelingen
In 1977 kreeg de RSA-methode wereldwijde bekendheid door RSA-129, weergegeven in de afbeelding hierboven. Een van de eerste versleutelingsmethoden die de besproken publieke sleutel gebruikte. Deze is in 1994 gekraakt.
De National Security Agency (NSA) kwam met het idee om de privacy en beveiliging van telefoongesprekken te verbeteren. Hiervoor werd in 1995 Secure Hash Algorithm 1 (SHA-1) in het leven geroepen, een 160-bits code. Google heeft deze in 2017 gekraakt.
Het kraken van SHA-1 heeft gevolgen voor ons huidige digitaal gebruik. Google heeft bijvoorbeeld de beveiliging aangepast voor het versturen van bestanden via Gmail en voor het opslaan van bestanden op Google Drive. Ook certificaten, die zorgen voor de veilige verbinding tijdens het browsen, die SHA-1 gebruiken zijn ongeldig verklaard.
Bedrijven als Google hebben hun beveiliging rond 2013 verhoogd van een 1024-bits code naar een 2048-bits code. De vraag is hoelang het duurt voordat de 2048-bits code wordt gekraakt. De rekenkracht groeit jaarlijks en daarbij zijn er de quantumcomputers. Worden er betere methoden gevonden voor het controleren van priemgetallen? Over twintig jaar is die vraag misschien beantwoord. Voor nu moeten we ons telkens de vraag stellen of websites en programma’s hun beveiliging hebben aangescherpt en of gebruik hiervan voldoende veilig is.
Stef Joseph-Kruyswijk (1981) is net begonnen met de Master Science Education en Communication (MSEC) aan de Universiteit Utrecht. Dit combineert hij met een baan als docent informatica, waar hij al het geleerde van de opleiding direct in de praktijk toepast. Zijn interesse voor priemgetallen was de aanleiding voor het schrijven van bovenstaand artikel. Het artikel is geschreven voor het vak Communicating Science to the Public.





