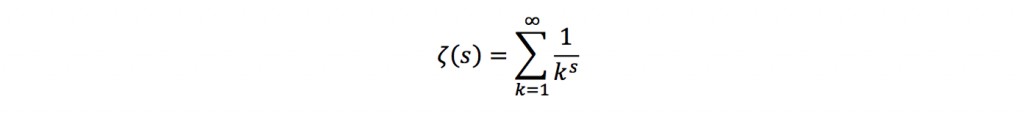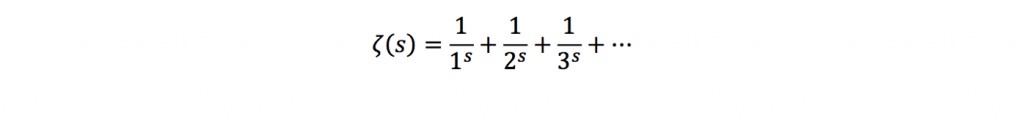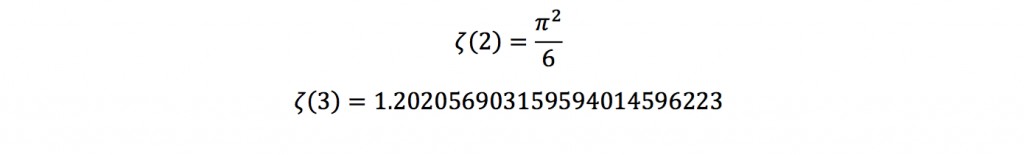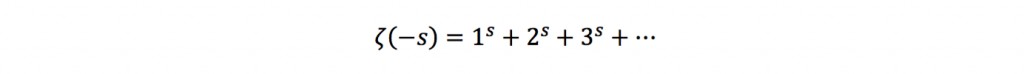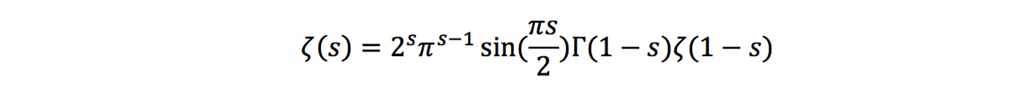De wiskundige Michael Atiyah beweert één van de belangrijkste wiskundige problemen te hebben opgelost. Maar is dat ook echt zo?
Groot nieuws in de wereld van de wiskundigen: geniaal wiskundige Michael Atiyah beweert een bewijs voor de Riemann-hypothese gevonden te hebben! De meeste mensen die niet verder gekomen zijn dan de wiskundelessen op de middelbare school of wat statistiek in het hoger onderwijs en zich verder niet interesseren voor wiskunde, zullen nu wellicht snel verder bladeren in het nieuwsoverzicht en denken dat dit vast over één of andere veel te ingewikkelde fundamentele wiskundige formule gaat. Dat klopt. Het is één van de meest ingewikkelde problemen in de wiskunde en daarom is de oplossing 1 miljoen euro waard. En toch is het zeker de moeite waard om je in de Riemann-hypothese en de claim van Atiyah vast te bijten.
De Riemann-Zèta-functie
Het beste is om gelijk met de deur in huis te vallen door de Riemann-Zèta-functie te laten zien:
Dit beest vertelt ons dat we een sommatie hebben van 1 tot oneindig over k voor de variabele s. Als dit nog steeds niet duidelijk is, wordt het met deze notatie misschien duidelijker:
Deze sommatie gaat dus door tot en met oneindig. Je intuitie zegt je nu misschien dat deze som altijd tot oneindigheid optelt, maar dit is niet zo. Dit is wel zo voor s=1, maar er komen verrassende getallen uit als je s verandert. Zo krijg je bijvoorbeeld voor s=2 en s=3:
Tot zover hebben we het dus over reële positieve getallen en de Riemann-Zèta-functie was op deze manier al bekend bij Leonhard Euler (1707-1783). Overigens als je je nu afvraagt wat reële getallen zijn: dit zijn alle bij ons bekende getallen waaronder breuken, gehele getallen, maar ook ????, alle machten en wortels. De Riemann-Zèta-functie heeft veel interessante uitkomsten voor verschillende positieve gehele getallen, maar als je negatieve getallen gaat invullen krijg je voor willekeurig negatief getal -s:
Dit lijkt opnieuw op te blazen tot oneindig voor elke s. Dit ziet er daarom niet zo nuttig uit, maar daar dacht Bernhard Riemann (1826-1866) anders over. Hij leidde af dat de Riemann-Zèta-functie namelijk omgeschreven kan worden tot:
Deze alternatieve vergelijking noemt men in de wiskunde een functionaalvergelijking, waarin de vergelijking uitgedrukt wordt in andere vergelijkingen, zoals hier de Γ-functie. Het doet er verder niet toe wat hier allemaal staat, maar het is alleen belangrijk om te weten dat nu voor de waardes voor s waar oneindig uitkwam er nu wel een eindig getal uitkomt. Deze manier van omschrijven van een vergelijking heet ook wel een analytische continuatie. Dit geldt alleen nog niet voor s=1, hier blijven we steken op een oneindige uitkomst. Met deze nieuwe analytische voorzetting kan je dus naast de positieve getallen die we al zagen, nu ook negatieve getallen invullen voor de Riemann-Zèta-functie. Nu blijkt met deze notatie van de Riemann-Zèta-functie voor s=-1 de uitkomst -1/12 te zijn en voor alle negatieve even getallen wordt de Riemann-Zèta-functie zelfs 0! Dit laatste kan je zelf misschien wel inzien door uit je middelbare school-wiskundekennis terug te halen dat sin(???? ⋅ ????) = 0 voor ???? gelijk aan een geheel getal.
Om de “ingewikkeldheid” nog verder uit te breiden, kun je ook voor s complexe getallen invullen. Op school heb je misschien nog geleerd dat je nooit de wortel kunt trekken uit -1, maar wiskundigen dachten daar op een gegeven moment anders over en kwamen op het idee om de reële getallen uit te breiden met getallen waarin negatieve wortels wel bestaan. Dit werd geïntroduceerd door de Italiaan Rafael Bombelli (1526-1572). Het is niet voor niets dat we dit complexe getallen noemen, want dit maakt de wiskunde nog complexer dan het voor ons menselijk brein al is. Simpel gezegd is een complex getal een reëel getal plus een imaginair getal, wat een hoeveelheid maal √−1 is. Deze wortel van -1 noemt men ook wel ????. Een voorbeeld van complex getal is dus 5 + 3???? of in het algemeen ???? + ????????, waar ???? en ???? reële getallen zijn en ???????? het imaginaire deel vormt. Het is makkelijker om dit iets inzichtelijker te maken door dit voor te stellen als een punt in het zogeheten complexe vlak met coördinaat (5,3), of in het algemeen (????, ????). Dus een x-as en een y-as, waar x de reële as is en y de imaginaire as.
Riemann-hypothese
Het introduceren van complexe getallen voor de Riemann-Zèta-functie is het moment waarin de functie erg ingewikkeld en voor wiskundigen dus interessant wordt. Hier zal Riemann in 1859 ook zo over gedacht hebben toen hij “Über die Anzahl der Primzahlen unter einer gegebenen Grösse” publiceerde en daarin een relatie tussen de nulpunten van de Riemann-Zèta-functie en de verdeling van priemgetallen – je weet wel, die getallen die alleen deelbaar zijn door zichzelf en door 1 – vaststelde. De nulpunten voor de negatieve even getallen die we zojuist al zagen, worden de ‘triviale nulpunten’ genoemd. De ‘niet-triviale nulpunten’ zijn de nulpunten die hier van belang zijn. Dit zijn een oneindig aantal getallen die met hun reële deel tussen 0 en 1 liggen. Nu komen we dan eindelijk bij de hypothese. Er is namelijk een heel sterk vermoeden dat het gaat om alle getallen met een reëel deel gelijk aan 1⁄2 en een imaginair deel gelijk aan it, waar t een willekeurig reëel getal is. Tot zover genoeg wiskundig hersengekraak.
Het oplossen van de Riemann-hypothese kan leiden tot een beter begrip van de verdeling van priemgetallen en kan nieuwe deuren openen in bijvoorbeeld de quantummechanica en de stochastiek. Hoezo is de Riemann-hypothese eigenlijk nog niet bewezen, we hebben toch ontzettend rekenkrachtige computers? Ja, klopt. Computers maken het vermoeden dan ook sterker, maar een waterdicht wiskundig bewijs is er nog altijd niet. Dit is waar Michael Atiyah in het verhaal komt als de zoveelste persoon die deze hypothese probeert te bewijzen. Wiskundigen breken zich er het hoofd al over sinds Riemann er mee kwam, maar zeker toen de Duitse wiskundige David Hilbert (1862-1943) tijdens het Internationaal Wiskundecongres in 1900 kwam met een lijst van 23 wiskundige problemen die voor het einde van de 20e eeuw moesten worden opgelost. Op nummer acht stond de Riemann-hypothese. De oplossing was nog niet gevonden in de 20e eeuw, dus kwam de Riemann-hypothese terug op de lijst van de Milleniumprijsproblemen. Dit is een lijst opgesteld door The Clay Mathematics Institute uit Cambridge, waarop zeven problemen uit de wiskunde en natuurkunde staan. Michael Atiyah was één van de twee personen die de lijst presenteerde op 24 mei 2000. Ditmaal is niet alleen de eer de prijs, maar ook een bedrag van 1 miljoen dollar per probleem. Van de zeven is er tot nu toe nog maar 1 probleem opgelost, dus de Riemann-hypothese zou het tweede kunnen zijn.
Atiyah heeft zijn bewijs grofweg geschetst tijdens een conferentielezing in Heidelberg (Duitsland). Dit werd live gestreamd en het bewijs dat hij daar toonde was te grof om er nog iets zinnigs over te zeggen. Daarnaast ging er op internet een artikel rond waar de ideeën van Atiyah wat dieper uitgelegd werden, maar nu al zagen een heleboel wiskundigen er fouten en gaten in. Verder heeft Atiyah nog geen compleet bewijs genoteerd. Dus het vertrouwen in Atiyah en het hebben van een bewijs is daarom aan het vervagen. Desalniettemin mogen we hem niet onderschatten, hij heeft namelijk al een heel belangrijke rol in de wiskunde gespeeld en daarnaast enkele grote wiskundige prijzen gewonnen, zoals de Fields-medaille (1966), de Copley Medal (1988) en de Abelprijs (2004). Toch kunnen we een nieuwe hypothese introduceren, waarin we stellen dat Michael Atiyah op 89-jarige leeftijd de Riemann-hypothese onopgelost laat…
Jurjen de Jong (1993) heeft een bachelor wiskunde en bachelor natuurkunde behaald in Utrecht en een master wiskundige natuur-en sterrenkunde in Gent afgerond. En nu rondt hij de master-na-master in Space Studies in Leuven af met een stage bij de ESA. Jurjen leest graag over de verschillende ontdekkingen en ontwikkelingen op wetenschapsgebied en door er over te schrijven hoopt hij zijn kennis te delen met een groter publiek. Later hoopt hij een baan in de ruimtevaartsector te krijgen. Eerder verscheen van Jurjens hand al dit interessante artikel waarin hij uitzoekt of het nodig is dat ook de ruimtevaart groener wordt. Ook zocht hij voor Scientias.nl uit of de ruimtelift werkelijk toekomst heeft. Recent publiceerde hij ook een artikel over de Parker Solar Probe: een ruimtesonde die binnenkort de zon gaat ‘aantikken’.